Closeness (mathematics)

In topology and related areas in mathematics closeness is one of the basic concepts in a topological space. Intuitively we say two sets are close if they are arbitrarily near to each other. The concept can be defined naturally in a metric space where a notion of distance between elements of the space is defined, but it can be generalized to topological spaces where we have no concrete way to measure distances.

The closure operator closes a given set by mapping it to a closed set which contains the original set and all points close to it. The concept of closeness is related to limit point.

1 Definition
2 Properties
3 Closeness relation between a point and a set
4 Closeness relation between two sets
5 Generalized definition
6 See also

Definition

Given a metric space 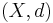$(X,d)$ a point $p$ is called close or near to a set $A$ if

$d(p,A) = 0$ ,

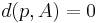where the distance between a point and a set is defined as

$d(p, A)�:= \inf_{a \in A} d(p, a)$ .

Similarly a set $B$ is called close to a set $A$ if

$d(B,A) = 0$

where

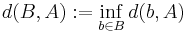$d(B, A)�:= \inf_{b \in B} d(b, A)$ .

Properties

if a point $p$ is close to a set $A$ and a set $B$ then $A$ and $B$ are close (the converse is not true!).
closeness between a point and a set is preserved by continuous functions
closeness between two sets is preserved by uniformly continuous functions

Closeness relation between a point and a set

Let $A$ and $B$ be two sets and $p$ a point.

if $p$ is close to $A$ then $A \neq \emptyset$
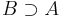if $p$ is close to $A$ and $B \supset A$ then $p$ is close to $B$
if $p$ is close to $A \cup B$ then either $p$ is close to $A$ or $p$ is close to $B$

Closeness relation between two sets

Let $A$ , $B$ and $C$ be sets.

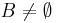
if $A$ and $B$ are close then $A \neq \emptyset$ and $B \neq \emptyset$
if $A$ and $B$ are close then $B$ and $A$ are close
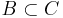if $A$ and $B$ are close and $B \subset C$ then $A$ and $C$ are close
if $A$ and $B \cup C$ are close then either $A$ and $B$ are close or $A$ and $C$ are close
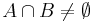if $A \cap B \neq \emptyset$ then $A$ and $B$ are close

Generalized definition

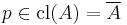The closeness relation between a set and a point can be generalized to any topological space. Given a topological space and a point $p$ , $p$ is called close to a set $A$ if $p \in \operatorname{cl}(A) = \overline A$ .

To define a closeness relation between two sets the topological structure is too weak and we have to use a uniform structure. Given a uniform space, sets A and B are called close to each other if they intersect all entourages, that is, for any entourage U, (A×B)∩U is non-empty.